邻接矩阵
邻接矩阵是图的表示方法之一。这种数据结构表示图结构,简单清晰,容易理解。下面介绍什么是邻接矩阵以及如何用邻接矩阵表示图结构。
邻接矩阵和图
我们看一个无向图的例子:
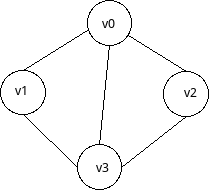
这个结构很简单,只有四个顶点。我们想要表示一个图结构,实际上就是想办法用一个数据结构,将这个图的顶点和边表示出来。邻接矩阵是这样设计的:
v0 v1 v2 v3
v0 0 1 1 1
v1 1 0 0 1
v2 1 0 0 1
v3 1 1 1 0
一个矩阵的行和列都表示图的所有顶点,比如:[v0,v1]这个位置的值为1,就代表顶点v0和v1之间是连接的,为0则代表两个顶点不连接。
我们发现,无向图中,由于没有方向,如果[v0,v1]为1,那么[v1,v0]也为1,最终导致的结果就是这个矩阵的对称的。
那么对于有向图,无非就是在上面的基础上修改一下了:
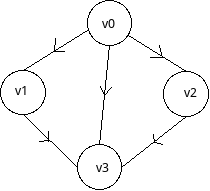
我们规定[v0,v1]值为1表示v0有一条有向边指向v1,而[v1,v0]值为0,因为v1没有一条有向边指向v0。
在邻接矩阵中,我们可以规定,行坐标表示源节点,列坐标表示目标节点。当然反过来也没问题。
那么结果就是这样了:
v0 v1 v2 v3
v0 0 1 1 1
v1 0 0 0 1
v2 0 0 0 1
v3 0 0 0 0
邻接矩阵的适用场景
当矩阵很大时,如果矩阵比较稀疏(也就是说顶点很多,但是边比较少),这时使用邻接矩阵十分浪费空间,因为无论有多少条边,我们都必须表示顶点数的二次方大小的矩阵。
但相反的情况,矩阵不是很大,也不是稀疏矩阵,此时使用邻接矩阵就很方便了,因为我们可以用定长二维数组表示矩阵,我们直接使用类似arr[x][y]的方式就能随机访问任意一个矩阵值(也就是图的边)。
作者:Gacfox
版权声明:本网站为非盈利性质,文章如非特殊说明均为原创,版权遵循知识共享协议CC BY-NC-ND 4.0进行授权,转载必须署名,禁止用于商业目的或演绎修改后转载。