队列

队列是一个应用十分广泛的数据结构，和栈类似，也是可以基于任何一种线性表结构来实现。栈的特点是后进先出，队列正相反，是先进先出。

队列的一个最常见的使用场景就是GUI程序，我们点击界面上的一个区域，或是键盘按下某个键，实际上是不能立即响应的，因为如果代码写成立即对操作做出响应，如果CPU运行较慢，后一个操作就可能覆盖前一个操作。因此我们需要一个容器存储所有的操作，响应操作的代码从容器中按顺序或优先级读取操作，依次响应，队列就是满足这种需求的数据结构。

环形队列和链式队列

和栈相同，队列的基本操作也有push进队列，poll出队列，peek查看队列头元素，clear清空队列，isEmpty队列是否为空。

根据队列的特点，用数组实现时，队列起始位置不一定是数组索引0的位置，队列的元素还可能跨过数组最后一个元素，又从数组开头位置占用空间，因此我们需要在遍历队列时注意，遍历到数组最后一个元素时，跳至数组第一个元素（也就是把数组头尾连起来，规定arr[len-1]的下一个元素是arr[0]），而用链表实现代码就简单许多。但是究竟用数组还是链表，还应该根据实际需求，合理选择。数组实现的队列一般叫做“环形队列”，链表实现的队列我们叫做“链式队列”。

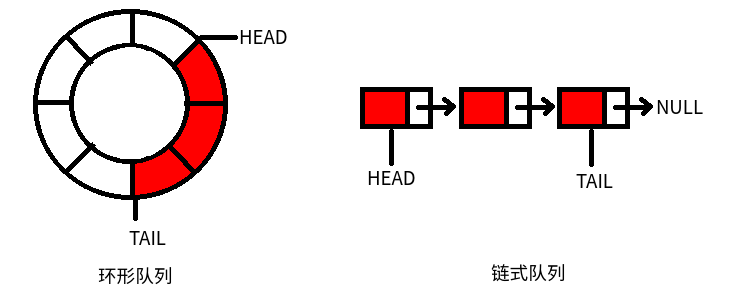
环形队列和链式队列的push和poll操作都是O(1)的，但是环形队列大小预先分配，链式队列频繁插入删除时，需要频繁分配和释放内存，有一定的性能开销。链式队列的指针域会额外占用一定的内存空间，但是不像环形队列一样预先分配内存，内存分配上更加灵活。

环形队列的实现

环形队列实现的关键就是下标的确定，和队列为空、队列已满的判断条件。

  • 如何判断队列为空：这里我们使用一个标志位isEmpty，当队列head == tail && isEmpty == false时，再poll一个元素队列就为空，此时设置空标志位；队列为空时，插入一个元素，就取消空标志位。
  • 如何判断队列已满：如果再插入一个元素，head == tail，那么队列当前已经是满的状态了，不允许插入。
  • 下标的判断：队列中不停插入元素，当前最后一个元素的数组索引是tail，那么再插入一个元素后，索引就是(tail + 1) % QUEUE_SIZE。

下面给出环形队列的实现代码

#include <stdio.h>
#include <stdlib.h>

#define QUEUE_SIZE 5

struct RingQueue
{
    int head;
    int tail;
    int isEmpty;
    int container[QUEUE_SIZE];
};

//初始化环形队列
void initRingQueue(struct RingQueue *rq);
//元素入队列
void push(struct RingQueue *rq, int i);
//元素出队列
int poll(struct RingQueue *rq);
//查看队列头部元素
int peek(struct RingQueue *rq);
//清空队列
void clear(struct RingQueue *rq);
//返回队列是否为空
int isEmpty(struct RingQueue *rq);
//打印队列（按照从队列头到尾的顺序，不是打印容器数组）
void display(struct RingQueue *rq);

int main()
{
    struct RingQueue *rq = malloc(sizeof(struct RingQueue));
    initRingQueue(rq);

    //测试
    push(rq, 1);
    display(rq);
    push(rq, 2);
    display(rq);
    push(rq, 3);
    display(rq);
    push(rq, 4);
    display(rq);
    push(rq, 5);
    display(rq);

    poll(rq);
    display(rq);
    poll(rq);
    display(rq);

    push(rq, 6);
    display(rq);
    push(rq, 7);
    display(rq);

    clear(rq);
    display(rq);

    free(rq);
    return 0;
}

void initRingQueue(struct RingQueue *rq)
{
    rq->head = 0;
    rq->tail = 0;
    rq->isEmpty = 1;
}

void push(struct RingQueue *rq, int i)
{
    if(rq->isEmpty)
    {
        rq->container[rq->head] = i;
        rq->isEmpty = 0;
    }
    else
    {
        int nextTailPosition = (rq->tail + 1) % QUEUE_SIZE;
        if(nextTailPosition == rq->head)
        {
            fprintf(stderr, "队列已满\n");
            exit(EXIT_FAILURE);
        }
        else
        {
            rq->container[nextTailPosition] = i;
            rq->tail = nextTailPosition;
        }
    }
}

int poll(struct RingQueue *rq)
{
    if(rq->isEmpty)
    {
        fprintf(stderr, "队列为空\n");
        exit(EXIT_FAILURE);
    }
    else
    {
        int result;
        if(rq->head == rq->tail)
        {
            result = rq->container[rq->head];
            rq->isEmpty = 1;
        }
        else
        {
            int nextHeadPosition = (rq->head + 1) % QUEUE_SIZE;
            result = rq->container[rq->head];
            rq->head = nextHeadPosition;
        }
        return result;
    }
}

int peek(struct RingQueue *rq)
{
    if(rq->isEmpty)
    {
        fprintf(stderr, "队列为空\n");
        exit(EXIT_FAILURE);
    }
    else
    {
        return rq->container[rq->head];
    }
}

void clear(struct RingQueue *rq)
{
    rq->head = 0;
    rq->tail = 0;
    rq->isEmpty = 1;
}

int isEmpty(struct RingQueue *rq)
{
    if(rq->isEmpty)
    {
        return 1;
    }
    else
    {
        return 0;
    }
}

void display(struct RingQueue *rq)
{
    if(rq->isEmpty)
    {
        printf("队列为空\n");
    }
    else
    {
        int p = rq->head;
        while(p != rq->tail)
        {
            printf("%d ", rq->container[p]);
            p = (p + 1) % QUEUE_SIZE;
        }
        printf("%d\n", rq->container[p]);
    }
}

链式队列的实现

链式队列实现比较简单，基本在链表基础上修改一下就行了，这里就不多写了。

优先队列

普通队列的特点是先进先出，优先队列则是人为的给每一个元素设置一个优先级，优先级最高的元素最先出队列。基于这个特点，我们会立刻发现使用线性的链表或是数组都不能满足这个需求，因为队列每插入一个元素，都要按照优先级进行排序，随机插入开销很大的数组肯定是不行的，链表也是需要多次遍历并比较大小才能做到，因此最好的实现是使用堆结构（当然堆也是数组或二叉链表实现的）。大根堆的堆顶永远是值最大的元素（这里的值指优先级），堆只能从堆顶删除元素，因此堆结构天然的就是一个优先队列。

具体见数据结构/堆章节。

作者：Gacfox
版权声明：本网站为非盈利性质，文章如非特殊说明均为原创，版权遵循知识共享协议CC BY-NC-ND 4.0进行授权，转载必须署名，禁止用于商业目的或演绎修改后转载。
Copyright © 2017-2024 Gacfox All Rights Reserved.
Build with NextJS | Sitemap